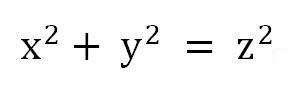数学科教諭 河合 治
タイトルを見て、「三平方の定理」の誤植ではないかと思った人もいるかもしれませんが、そうではありません。「三平方の定理」は、平面上、つまり、2次元の世界で成り立つ定理ですが、3次元の世界に拡張して考えると、同様の定理が成り立つのです。(ちなみに、「四平方の定理」は正式名称ではありません。また、知っている人も多いと思います。「究」というには全く値しないつまらない内容で申し訳ありません。)
「三平方の定理」
O(0, 0), A(a, 0), B(0, b) (a>0, b>0) とし、線分 OA, OB, ABの長さを、それぞれ x, y, z とすると、
「四平方の定理」
O(0, 0, 0), A(a, 0, 0), B(0, b, 0) C(0, 0, c) (a>0, b>0, c>0) とし、三角形OAB, OBC, OCA, ABCの面積を、それぞれX, Y, Z, Sとすると、
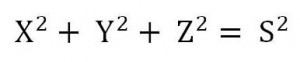 が成り立つ。
が成り立つ。
同様に、「五平方の定理」(4次元の世界で、4面体の体積を考える)、「六平方の定理」、・・・も成り立ちます。ぜひ、考えてみてください。
ともかく、本校生(に限らないとは思うが)は、指示されたことさえやればよいと思っている人が多いような気がします。ぜひ、積極的に色々取り組んでほしいものです。